Amikor 2010 augusztus 18-án ennek a bejegyzésnek a szövegét közzé tettem, akkor még a Higgs kísérletek 2012-ben "megtalált" aspiránsairól egyikünk sem tudhatott. Immáron két és fél év múltán azt mutatja a történelem, hogy még mindig érvényes az ábra alatti levezetés.
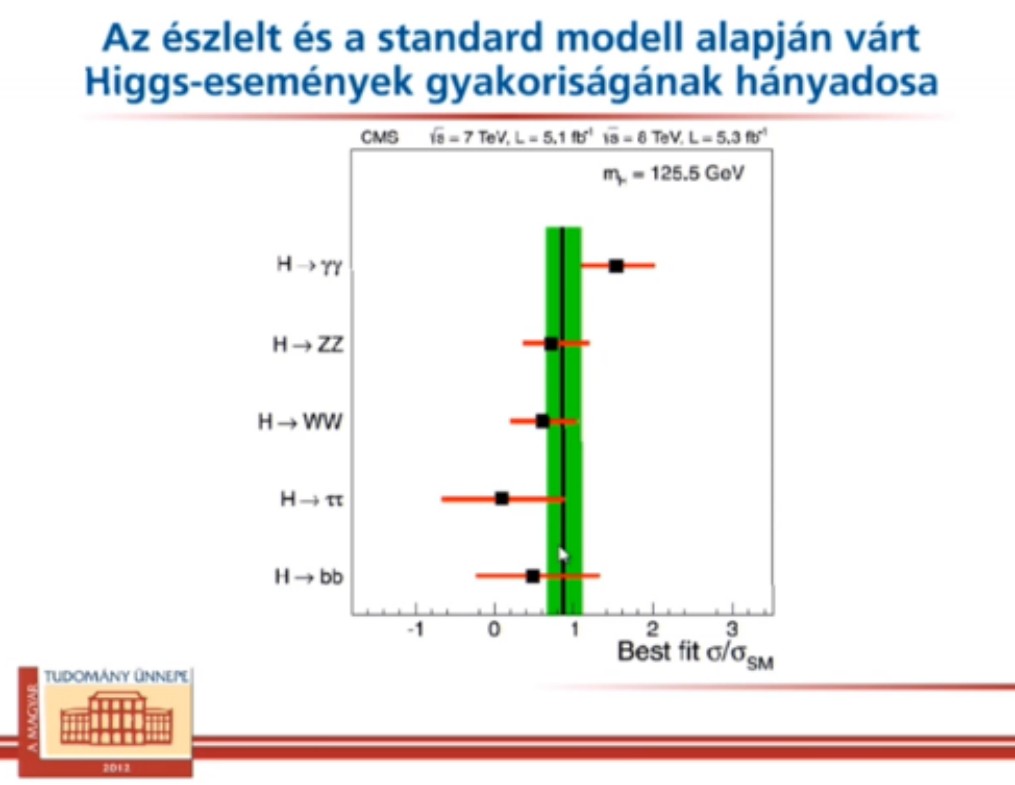
Miért szükséges vagy felesleges a Higgs keresése? - kérdezhetnénk.
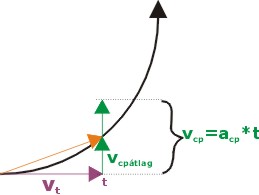
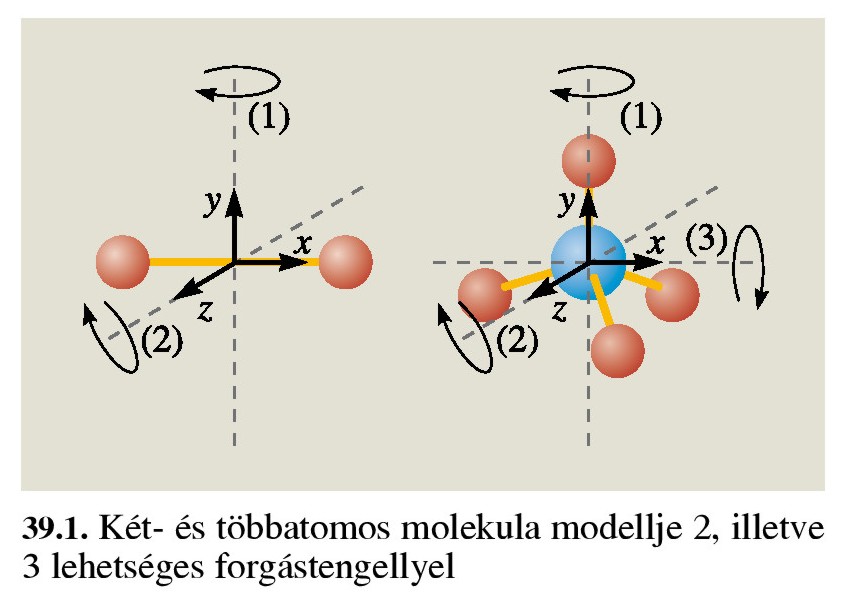
A mérési eredmények szerint a spin 0, 1 < 10 körüli.. azaz az ezzel keltett centripetális gyorsulás nagyon kicsi.. és az általa okozott kisugárzás azaz foton energia tíznek a mínusz nagyon sokadik hatványával jellemezhető.. A spinnel mozgatott részecske rész kerületi v sebességének függvényében energiát veszít.
ΔE=-4*Pi*Q²*(v/c)²*ß²*ß²/3/R ahol ß= c/d = 1/gyök(1-(v²/c²)), c a fénysebesség [3e8 m/s ]vákuumban, R a sugárzó részecskerész mozgási sugara a forgástengelyétől, Q a részecske elektrosztatikus töltése [C].
(Figyelem! Ez az R például egy elektron esetében a holon-spinon rendszer perdületi sugara és nem valamilyen keringési sugár! Valamint természetesen érvényes a függvény bármekkora nagyságú R esetében, mint például a ciklotronban haladó töltéshordozó részecskékre a ciklotron gyűrű sugara is lehet R.)
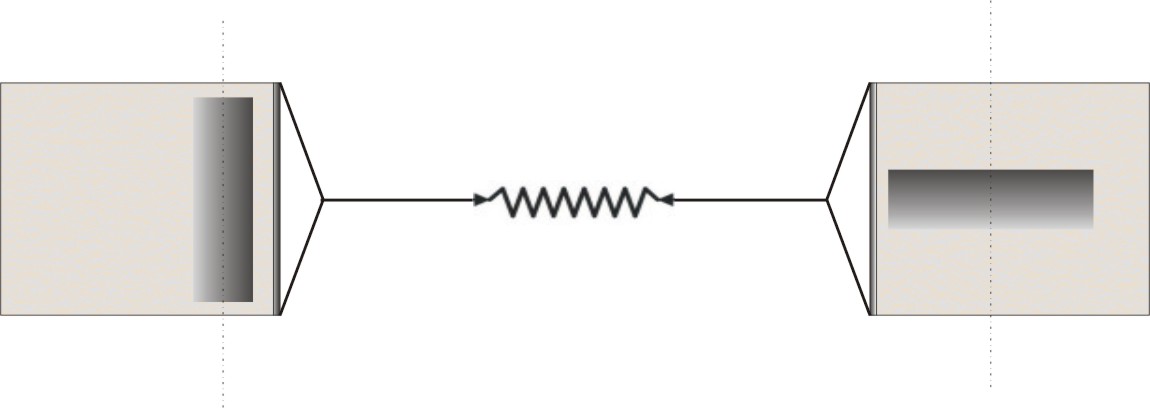
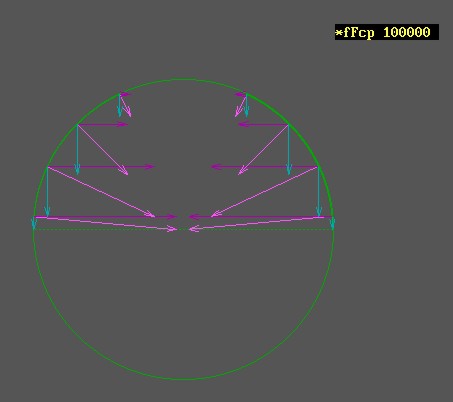
Az energia adagok impulzusai gömbszimmetrikusan távolodnak a részecskéktől, így eredőjük csak akkor zéró ha a részecskére mozgásállapotának megváltozását kényszerítő impulzus nem hat.
Amikor pedig gyorsulásra kényszerítjük, akkor ezzel a gyorsulás irányában és az ellentétes oldalán kisugárzott energia impulzusai a hatás-ellenhatás törvényéből valamint a relativisztikus Doppler jelenségéből következően eltérő nagyságúak, eredőjük a gyorsulás irányával szembeni irányba mutató vektorú erő.
Hiszen ez "maga a tehetetlenség!" Megtaláltam a Higgs bozont? Vagy csak azt, hogy miért nem kell lennie?
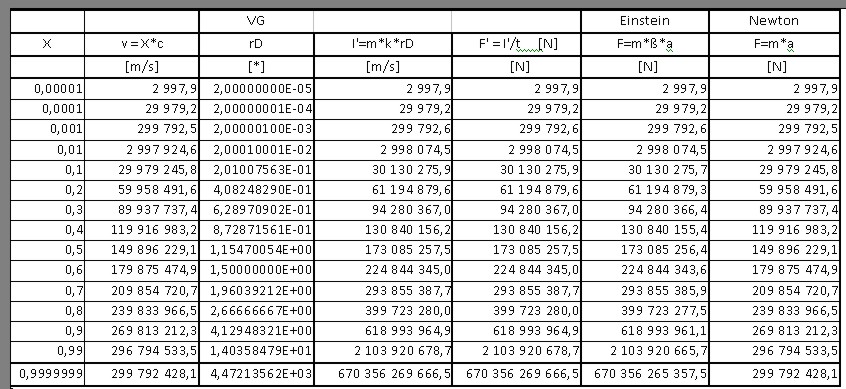
Azt tudjuk, hogy a fény sebessége c= 299792458,108 m/s
k [m/s] = 149 896 229,054 a tehetetlenségi faktor
m [kg] = 1,000000 nyugalmi tömeg
t [sec] = 1,000000 sebesség változás ideje a gyorsító rendszerben
A 'k' pontos értéke: k=2/c (= 1/ 6,6712819015597168713015141224781e-9 [m/s]
( Amely állandót közvetlenül számíthatjuk a relativisztikus Dopplerek különbözeteként:
v=1 [m]; m=1 [kg]; t=1 [s] és F=10 [N] behelyettesítésével. )
Ismerve, hogy egy m tömegre sugárzással ható impulzusok eredője a relativisztikus Doppler függvénye szerint függ a sebesség változás, azaz a gyorsulás mértékétől:
rD=(gyök((c+v)/(c-v))-gyök((c-v)/(c+v)))
ΔI= m*k*rD
F= ΔI/t
Miután a sugárzások impulzusa a haladási irányban I=I0*gyök((c+v)/(c-v)) értékűre növekszik, hátrafelé irányból pedig I=I0*gyök((c-v)/(c+v)) értékűre csökken,
az rD különbözetük adja az eredő impulzus nagyságot ΔI=I0*rD
Azaz a gyorsíthatóság tömeget érő sugárzások relatív Dopplerrel számolható egyensúlyától függ.
Más megfogalmazással a tömeg tehetetlensége nem a Higgs bozon műve, hanem tisztán a tömeg mozgatása során fellépő relativisztikus Doppler hatás következménye.
(Megjegyzések:
1. A táblázatot Excellel készítettem, így az Excel pontatlansága megjelenik a
fénysebesség közeli v sebességek esetén.
2. A tehetetlenségi faktor reciprokának jó közelítéssel század része a G gravitációs
állandó értéke. )
Ketten is javasolták, hogy a relativisztikus Doppler szorzók különbözeteként jobb lenne ha a rD= (2v/c)/gyök(1-(v²/c²)) alakot használnám, mert miután a k=c/2 így
I'=m* c/2*(2v/c)*γ ahol γ=1/gyök(1-(v²/c²)) a Lorentz transzformáció gammája
ezért I'=m*v*γ amiből az erő F=I'/t és F=m*v/t*γ azaz F= m*a*γ alakilag azonos Einstein által is felhasznált függvénnyel. ( Ezzel az új táblázatban szereplő értékek: Az átrendezéssel az Excel pontatlansága okozta eltérés valóban eltűnik.)
A v sebességre történő gyorsulás I' impulzus és F' erő igénye a táblázatban láthatóan azonos értékű a mérésekkel igazolt erő igénnyel (Einstein oszlopában található F erő igény helyességét CERN-ben mérésekkel ellenőrizték).
Tehát a mérések ezzel azt igazolták, hogy a tömegeken létrejövő impulzus párok eredője valóban azonos nagyságú erőt fejt ki tehetetlenségként megjelenve, mint a mérési tapasztalattal igazolt erőigény.
Ezzel bebizonyosodott, hogy a testek tömegének tehetetlenségét egyedül és kizárólagosan az impulzuspárok eredőjének a gyorsuláskor megjelenő értéke okozza. Nincs semmilyen olyan erőhatás amelyért felelősség tehető a feltételezett Higgs bozon.
A véleményeket a vertes.geza@gmail.com címen is várom.
"Túl tömény" ahogy írni szoktam erről a témáról. Akkor talán itt és most elkezdem a "szöveges" leírást..
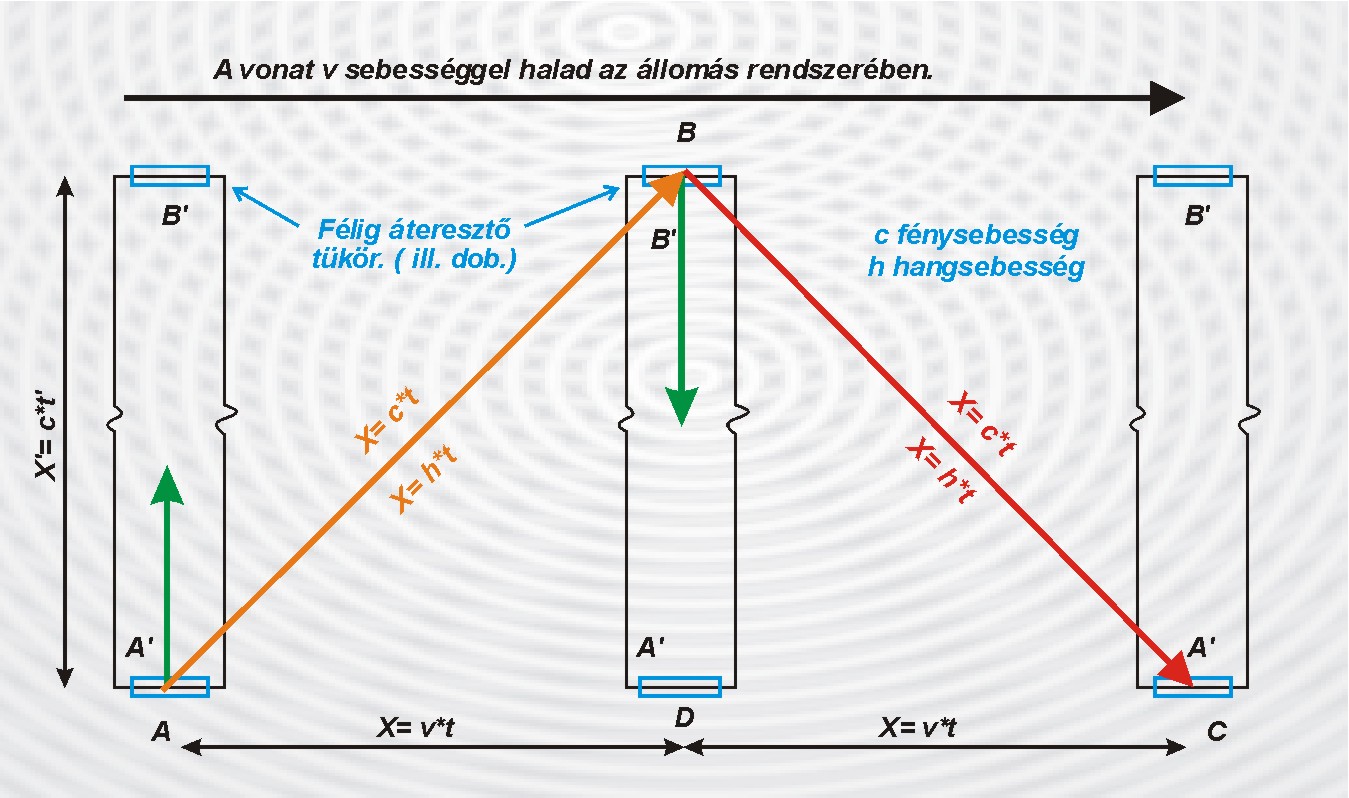
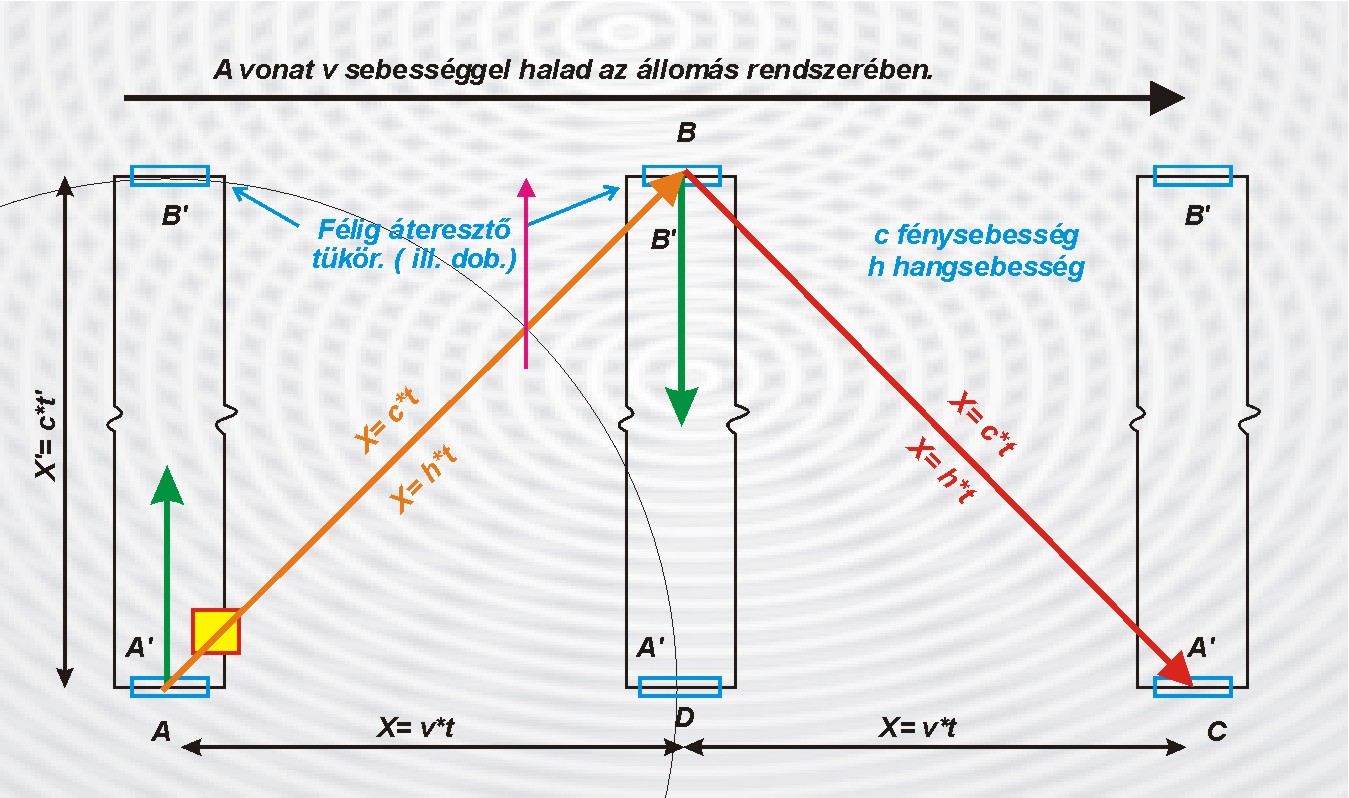
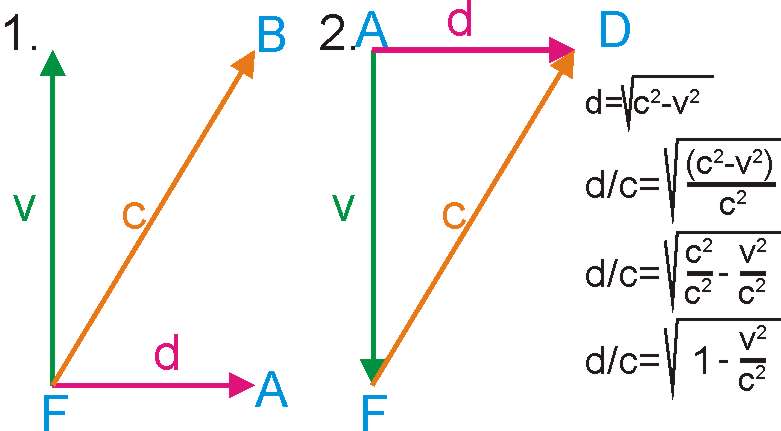
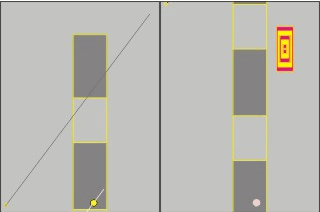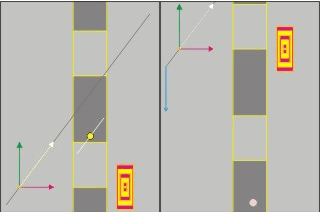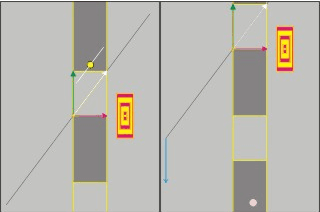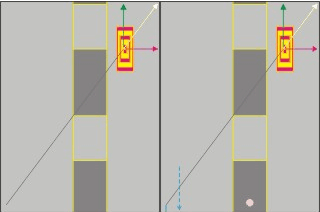
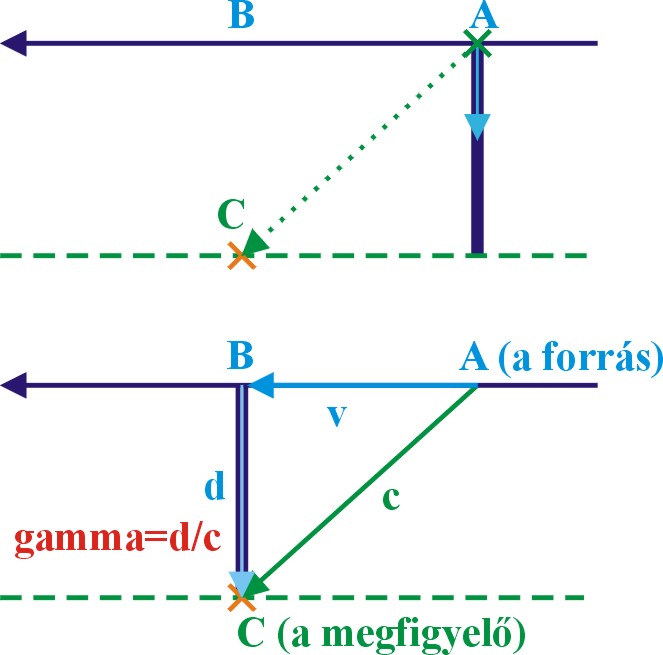
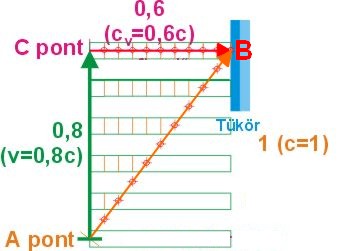
Mint kísérleti tapasztalatból tudjuk, a távoli tárgyakról akkor szerzünk tudomást, ha valamilyen jelhordozó jelenség, mint a hang vagy a fény hírt hoz róluk. Ezzel a jelhordozó jelenség a megfigyelés részesévé válik a tulajdonságai által. Hiszen minden jelhordozónak van saját sebessége, térbeli és időbeli eloszlása, kiváltó oka, jellemző energia sűrűsége és változási sebessége. Ezért ha egy távoli, hozzánk viszonyítva álló tárgy méretét szeretnénk meghatározni, akkor ha eléggé türelmesek vagyunk és van például a tárgy és köztünk olyan közeg amelyben a jel terjedhet, akkor megmérhetjük ezt a hosszot akár két zsinórral is, mint jeltovábbító eszközökkel..
Vagy akár egyetlen zsinórral is, mint mércével, ha közvetlenül a távoli tárgy mellett akad egy segítőnk aki a zsinórt-a mércét - odailleszti a távoli tárgy "nevezetes" pontjaihoz. Természetesen lehet a mérce anyagi hullám is, mint a hang, vagy anyagtalan energia csomag mint a fény. Csak az a fontos a pontos méréshez, hogy ismerjük a méréshez felhasznált "eszköz" illetve jelenség tulajdonságait, és bele tudjuk kalkulálni a kapott mérési eredményekbe. Így akár hang radarral vagy elektromágneses radarokkal is megmérhetjük egy tárgy méreteit a jel visszaverődési idejének megmérésével.
És/Vagy akár a visszavert jel irányának pontos észlelésével, mert ha az irányszög ismert, a távolság a visszaverődési idő méréséből szintén ismert, akkor egyszerű geometriai számításokkal meghatározható a tárgy pontjai közötti távolság.
A hétköznapi életben is ezt a mérést elvégezzük, néhány segéd mérce segítségével amikor például egy távoli ponton álló tárgy méretét becsüljük meg a "szemmértékünkkel".
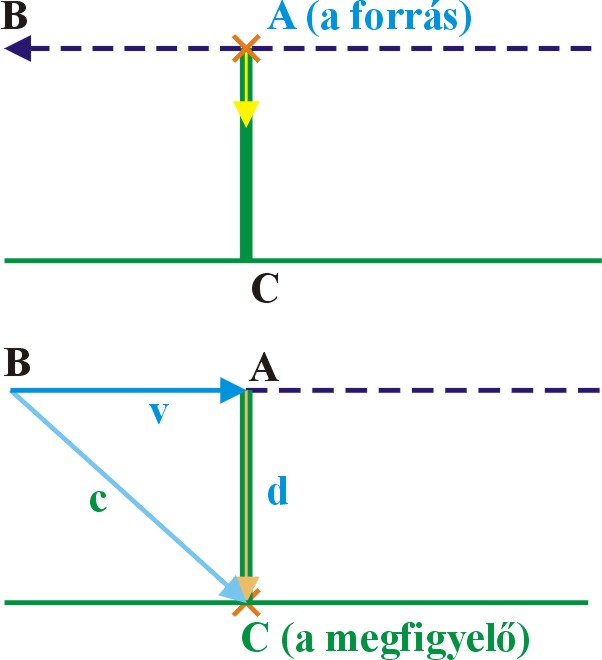
A tárgy és köztünk lévő távolságot a Föld felszínén lévő testek "sorba rakásával", és a méretet az irányszögek különbözetével. Sokszor az ismert tárgyak méreteit automatikusan felhasználjuk a távoli tárgy méretének meghatározására. Mint egy átlagos ember magassága, vagy egy szabványos oszlop mérete. A gondok akkor kezdődnek, ha a távoli tárgy mozog. Mert nehéz hozzá mérni még a környezetében álló, számunkra ismert méretű tárgyak méretéhez. A tapasztalat szerint minél nagyobb a mozgási sebessége, annál nagyobb az összehasonlítással járó hiba mértéke is. A mozgás következtében létrejövő összehasonlítási hibának a sebesség függését meghatározva, kapunk egy univerzálisan használható hiba javítási lehetőséget, más néven transzformálhatjuk a mozgás következtében hibásan megmért adatokat az álló környezetünkbe..
Azaz hiába van véges terjedési sebessége a mérésben közreműködő jelnek,
miután ismerjük a jel sebesség és a mozgási sebesség arányában létrejövő mérési hiba mértékét minden sebességen, az álló és a mérést segítő jel sebessége közötti teljes sebesség tartományban, ismerjük a javításhoz szükséges függvényt. Így a méréssel kapott hibás adatokat át tudjuk "transzformálni" az álló állapotú mérések világába, azaz a mozgás okozta hiba nélküli "világunkba".
Ezt én hiba javításnak, vagy kompenzálásnak nevezném, de volt egy Einstein nevű gondolkodó, aki úgy képzelte, hogy jobb ha erre a mérési hibára felépít egy elmélet rendszert, vagy ahogy a tudósok nevezik, egy fizikai modellt. Sajnos az a nagy baj, hogy miután minden ismeretünk, filozófiai értelemben csak egy modellje a bennünket körül vevő világnak, sokan úgy képzelik, hogy a modellek ha a világunk jelenségeire részben illenek, azaz a mérési tapasztalatokkal egyező eredményeket IS adnak, akkor bizonyára minden más esetre is érvényesek. Azaz akkor érvényesek az egész világ, minden jelenségére, nem csak a mérési eredményekkel azonos eredményeket produkáló részére. Így a tévedést tovább görgetve, sokan azt is feltételezik, hogy a modellből következő-következtethető jelenségeket a világunkban meg fogjuk találni. Azaz ha egy modell nem zárja ki, a semminek, a térnek a görbíthetőségét és tetejében sorozatosan a koordináta rendszer osztásainak deformálását, "görbületét" emlegeti, mert nem a sokak számára szokásos derékszögű koordináta rendszerbeli leírást, hanem a Gauss féle görbült koordináta rendszert használja a leíráshoz, akkor ebből sokan úgy vélik, hogy maga az üres tér, az idővel együtt, azaz a "téridő" görbül el az energia, vagy éppen a tömegek kisugározta gravitációs "negatív" energia hatására. Pedig csak az ábrázolásra használt koordináta rendszer osztásainak sűrűségét befolyásolják ezek az említett hatások, nem pedig a tér és idő tulajdonságait. Amit még látványosabban mutat az is, hogy ugyanazon tömeg által okozott "téridő görbületen" különféle sebességgel egyszerre áthaladók számára, teljességgel eltérő, akár nagyságrendekkel más és más lesz ugyanazon "téridő görbület". Pedig ha valóban a téridő görbült volna el a tömeg hatására, akkor mindegyik szemlélő számára azonos mértékűnek kellene lennie a görbületnek.. de nem azonos. Persze igaz! Minden relatív! Azaz Einstein már az előző művében leszögezte, hogy ugyanaz a jelenség, minden, egymástól eltérő mozgásállapotú megfigyelő számára másként jelenik meg.. Más hosszakkal, más időkkel.. Azaz amivel kezdtem a mozgók leírását, minden egymástól eltérő sebességű megfigyelőhöz a jeltovábbítás sebességének végessége következtében más mértékben torzult mérési eredményt okozó jel érkezik. Azaz nem a téridő egyedi, minden, egymástól eltérő körülmények között lévő megfigyelő számára, hanem csak a saját maga által használt mércéi, és ebből következően a kizárólag saját maga által alkalmazott koordináta rendszerének osztásai egyediek.. Azaz a tér sem az idő sem deformálódik, csak a leírására használt mércék, koordináta rendszerek "deformálódnak". Ebből pedig az következik, hogy bár sokan szeretnének hinni az időutazás, a múlt és a jövő összekuszálásának lehetőségében, de szerencsére erre soha senkinek sem lesz módja. A nagy távolságú, pillanat alatti utazások, a féregjáratok létének képzetével, szintén nagyon csábító hitet keltenek.. És bár az időutazás is és a féregjáratok létezésének lehetősége is közvetlenül az Einstein féle téridő görbület lehetőségéből következne..
Sajnos, vagy szerencsére ezek egyike sem lehetséges a fizikai valóságban, mert nem a fizikai valóságnak, hanem a fizikai valóságot nagyon rosszul leíró modellnek a következményei. Olyan nagyon rettenetesen rosszul leíró modell következményei, amely modell megenged ilyen hatalmas tévedéseket.. Szerencsére mi már tudjuk, hogy a relativitás mint modell nem más, mint a jeltovábbítási sebesség okozta mérési hiba kompenzálására készült függvényeket: hamisan, félrevezetően, és mondjuk ki: gonosz-csaló módon kitekert félremagyarázására épített csalás. Vegyünk egy egyszerű példát a csalás leleplezésére:
"F, m, a, ß" F erő, m tömeg, a gyorsulás és ß a Lorentz faktor..
Newton óta tudjuk, hogy F=m0*a összefüggés érvényes, azaz a gyorsításhoz szükséges erő nagysága egyenesen arányos a tömegnek és a gyorsulásnak a nagyságával. Lorentz méréseiből azt is tudjuk, hogy az erőhatás terjedési sebessége is csak fénysebességű, ezért a helyes erő függvényt: F = m0*ß*a alakban követi a v/ sebesség növekedését.. azaz a gyorsulást. Nagy kérdés, hogy ezt a ß-szorzót hova illesszük?
Einstein szerint m=m0*ß azaz a tömeg növekszik meg... Szerintem pedig a*ß azaz a tehetetlenség a relativisztikus Doppler hatására okoz növekvő ellenállást és az "m0" tömeg változatlan marad..
Hogyan lehetne eldönteni azt, hogy melyik álláspont a helyes?
Nagyon egyszerűen! Ha a relatív mozgás v sebességének növekedése az "m" tömeg növekedését okozná, akkor ezzel a gravitáló hatása is növekedne az "m" tömegnek.. Azaz ha Einstein elve érvényes, akkor ha a "v" sebesség közelít a "c" fénysebességhez, akkor az "m" tömegnek végtelen nagy gravitációja lenne..
Nos, a gravitáció, azaz az "m" tömeg súlyereje semennyit sem változik attól, hogy hozzá viszonyítva nagyon nagy v sebességgel, vagy akár c sebességgel mozog-e valami vagy nem mozog..
Nincs köze az m tömeg nagyságához a relatív mozgásnak. Ha most valaki azt mondaná, hogy ne a fény c sebességéhez hasonlítsuk, akkor oké.. hasonlítsuk a fény sebességét 99,999999%-ra megközelítő sebességű elemi részecskékhez.. Miután ilyen részecskék ezrei érnek minden kilogrammunkat, minden percben, a tömegünknek az einsteini elv szerint: (v=0,99999999c esetén) ß=7072 m=m0*ß=m0*7072 [kg]
azaz minden kilónk hét tonnát nyomna, akárhányszor elszáll mellettünk egy müon .. amelyhez relatív sebességünk v=0,9999999c Azaz szinte folyton sok ezer tonnásnak kellene lennünk..
Tehát ebből következik, hogy a relatív sebesség önmagában nem okoz tömeg növekedés, csak tehetetlenség növekedés okoz.
Na igen, de okoz-e tehetetlenség növekedést?
Gyorsítsunk F erővel egy testet majd szakítsuk meg a gyorsítást. A test tehetetlenségi pályán halad tovább.. Azaz önmagához viszonyítva áll.. Semmit sem tud a tömege az einsteini állítólagos tömegnövekedésről..
Ezért aztán, ha odakocog mellé egy kisegér és picinyke f erőcskével elkezdi nyomni az m0 azaz a nyugalmi tömeget, akkor a=f/m0 gyorsulást okoz rajta.. Sőt, még az is teljesen mindegy, hogy ez a gyorsulás és a korábbi gyorsulás iránya milyen mértékben függött össze.. Mert nincs semekkora jelentősége sem..
A kisegér okozta picinyke a=f/m0 gyorsulás ugyanazon függvényt követi mint bármelyik korábbi F erő okozta a=F/m0 gyorsulás. Azaz az einsteini tömegnövekedés, kamu.. Az einsteini tehetetlenség növekedés kamu..
Tehát a függvény m=m0*ß alakban biztosan rossz, hibás helytelen.
Na jó, de akkor csak a másik alak marad az F=m0* a*ß alak, mert az erőméréssel tudjuk, hogy m0*a*ß együtt ad helyes F erő értéket. Na de, mi az a*ß értelme? Miért lenne jó ez az alak?
Azt tudjuk, hogy minden test a rá ható változó gyorsulás hatására energiát sugároz ki.. Ezt a jelenséget például elektronokkal .. TV vagy mobil telefon antennákban gyorsításkor létrehozott foton kisugárzás formájában hasznosítjuk. Azaz gyorsulásra kényszerítjük az elektronokat és kisugározzák a TV adást vagy a mobilunkról azt az adást amely eljut a beszélgető partnerünk fülébe.. Ha ellenőrizzük a fentebbi állítást, akkor azt találjuk, hogy minden anyagban van elektron, és minden gyorsulásnak kitett elektron fotonokat sugároz ki..
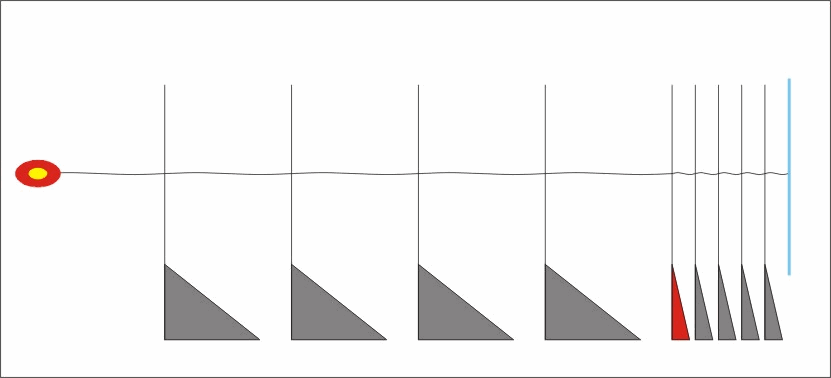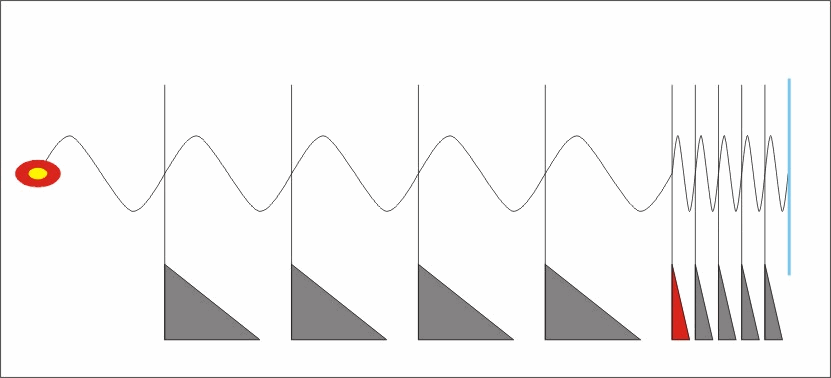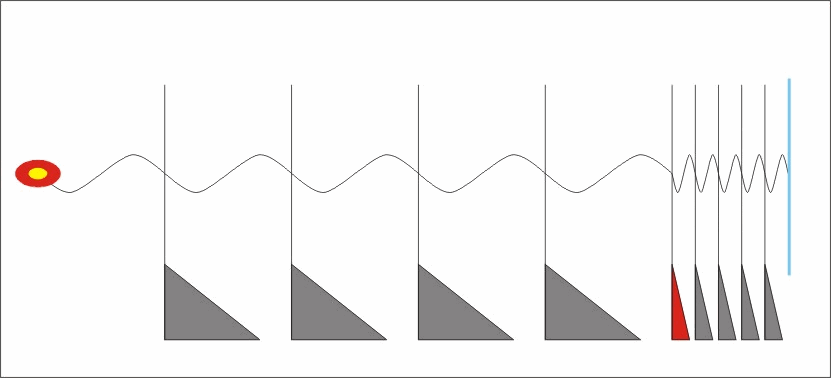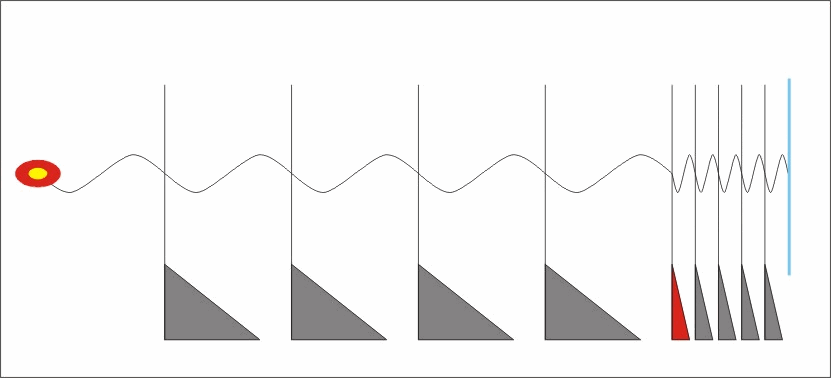
Ha tovább vizsgálódunk, akkor pedig azt tapasztaljuk, hogy minden elektromos töltéssel rendelkező részecske szintén foton kisugárzással válaszol a rá ható gyorsulásra.. Sőt! Ha még tovább vizsgálódunk, akkor azt tapasztaljuk, hogy a részecskék gyorsulását kizárólag a rájuk ható fotonokkal tudjuk létrehozni.. Azaz minden mozgás vagy foton kisugárzás vagy foton elnyelés következtében jön létre.. Vagyis minden mozgásállapot változást foton elnyelés vagy foton kisugárzás kísér. A mozgás állapot változás pedig egyben sebesség változást jelent.. Azaz például a nulláról v nagyságúra növekvő sebesség esetén a nulláról
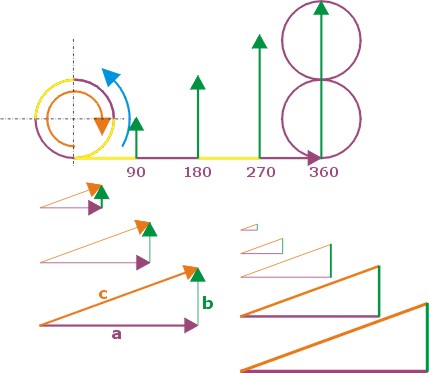
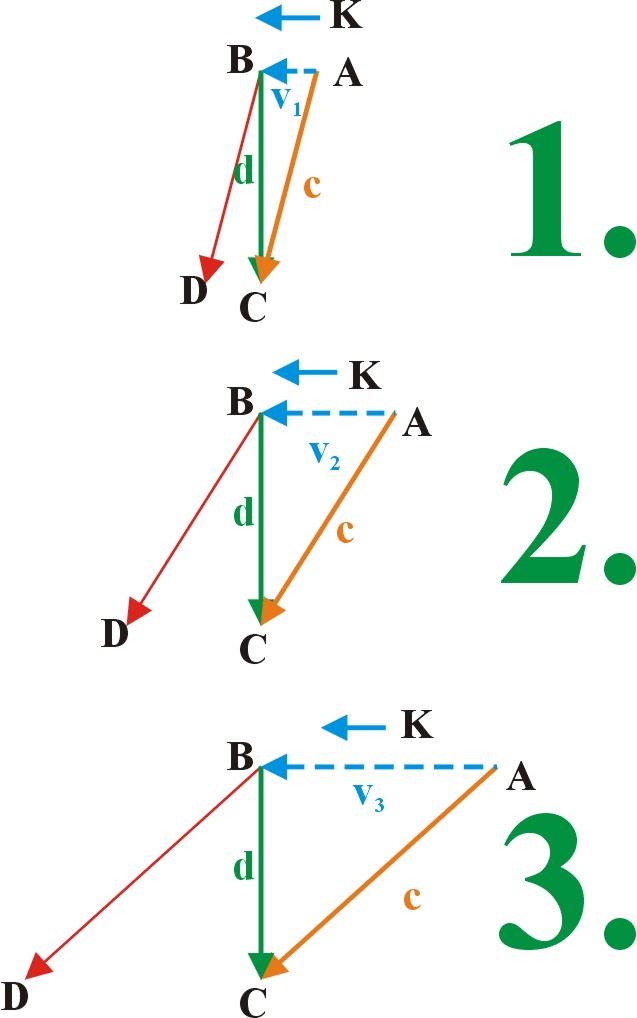
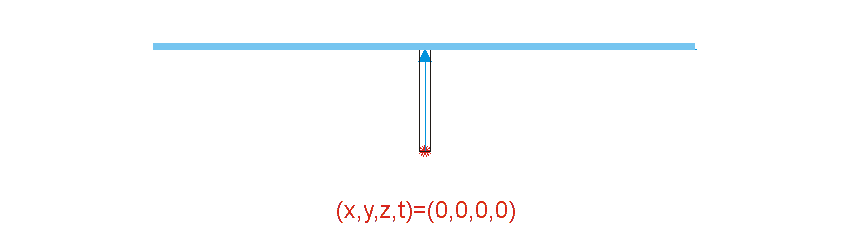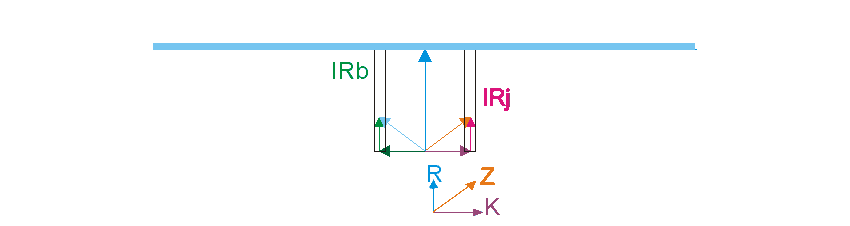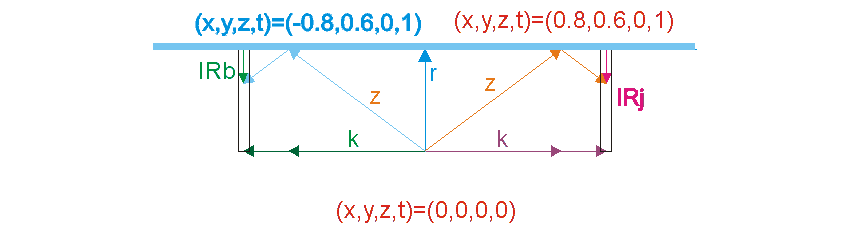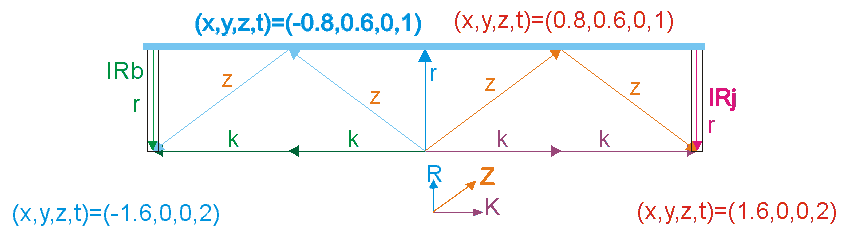
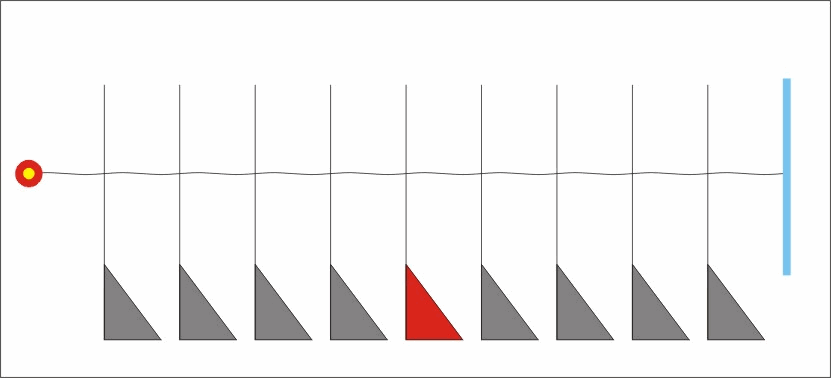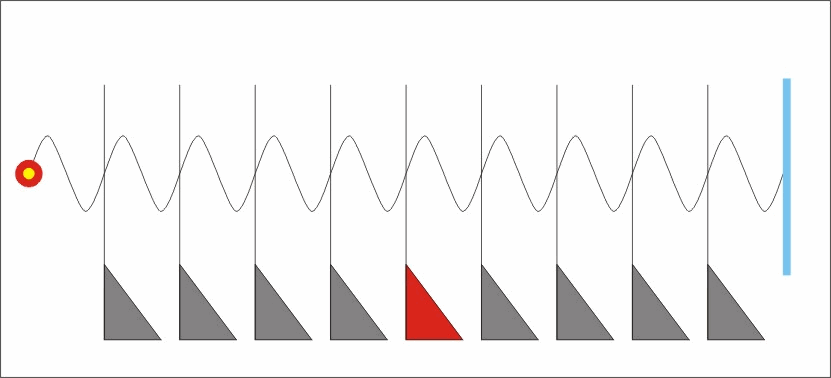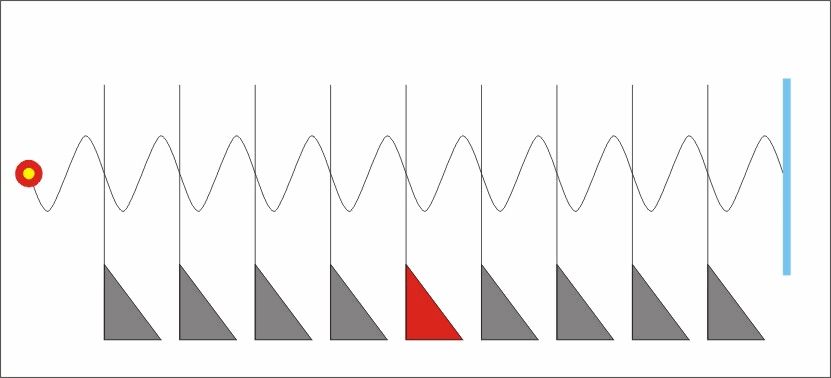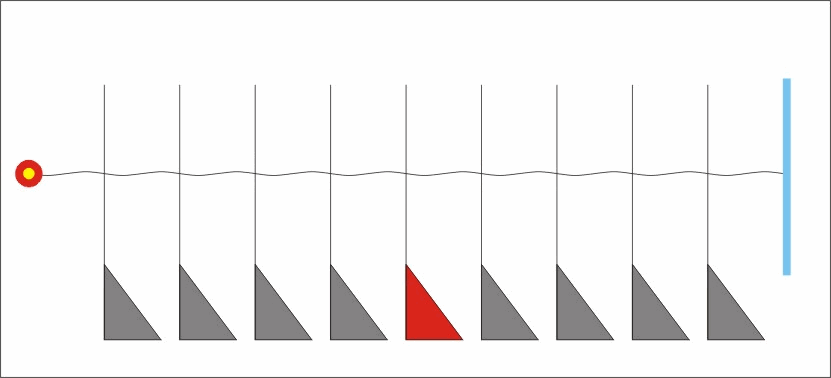
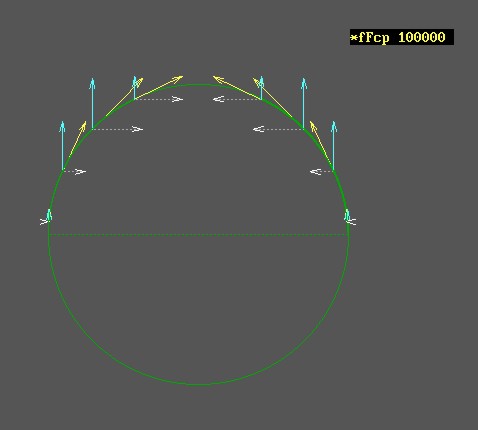
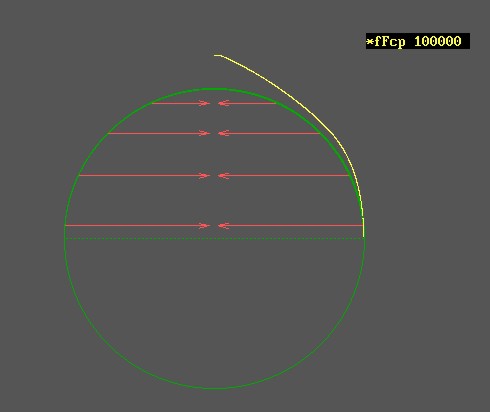
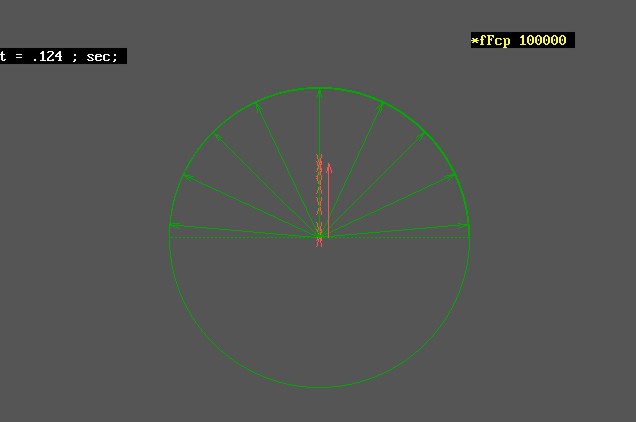
gyök((c+v)/(c-v)) -szeresére növekszik a kisugárzó oldali frekvencia, és ezzel a térben az impulzus és energia sűrűség is.. Vagyis ha elmozdulásra kényszerítünk egy testet, azaz ezzel sok sok részecskét, akkor mindegyikükre a mozgatás irányával szembeni oldalon rel. Doppler okozta impulzus sűrűsödés hat a saját maga által a gyorsulás hatására kisugárzott fotonok visszahatásaként, a másik azaz a távolodó oldalon pedig szintén a rel.Doppler következtében frekvencia csökkenés és ezzel impulzus és energia sűrűség csökkenés következik be.
Vagyis miután minden részecske spinnel, azaz perdülettel rendelkezik.. És a perdület bizony centripetális gyorsulás nélkül nem lehetséges, ezért minden spinnel rendelkező részecske folyamatosan foton sugárzó.. és ebből következően, minden gyorsulás esetében a folyamatosan kisugárzott fotonjaikat a rel.Doppler a térben, időben sűríti és a másik oldalon ritkítja.. Ezen két oldali impulzusok eredőjét képezve megkapjuk azt az impulzust, amellyel minden tömeg szembeszáll a rá ható gyorsító hatással..
azaz a szembe oldalon m*k*i*gyök((1+(v*c))/(1-(v/c)))
a "hátsó" oldalon pedig m*k*i*gyök((1-(v*c))/(1+(v/c)))
A két impulzus eredője pedig:
I =m*k*i*( gyök((1+(v*c))/(1-(v/c)))-gyök((1-(v*c))/(1+(v/c)))) ahol k=c/2
azaz egyszerűsítésekkel
k*( gyök((1+(v*c))/(1-(v/c)))-gyök((1-(v*c))/(1+(v/c)))) = v/gyök(1-(v²/c²))
azaz mivel ß=1/gyök(1-(v²/c²))
k*( gyök((1+(v*c))/(1-(v/c)))-gyök((1-(v*c))/(1+(v/c)))) = v*ß
ahol k=c/2 és a rel. Dopplerek különbözete pedig: (2*v/c)*ß azaz c/2*2*v/c*ß = v*ß
így I =m*dv*ß impulzus hat ellent dv sebesség változásnak ezért
a gyorsulás a=dv/dt azaz az erő a rel. Doppler különbözetek hatásaként
F= m* a*ß
Vagyis, ismert fizikai mérési tapasztalat szerint, a testek tömegének tehetetlensége a relativisztikus Doppler mértékétől függő időben és térben bekövetkező impulzus "sűrűsödés és ritkulás " következménye. Azaz ha befejezzük a gyorsítást, akkor a test tömege éppen annyi mint a gyorsítás előtt volt.. Sőt a tehetetlensége sem változik.. Jöhet az a kisegér és a picinyke f erejével létre tudja hozni a Newton függvénye szerinti gyorsulást..
Na igen! - mondhatnánk.. Minden spinnel együtt jár a centripetális gyorsulás, akkor - mint írtam, - folyamatosan sugároz minden spinnel rendelkező részecske fotonokat.. Viszont ilyen "világítást" nem tapasztalunk! Akkor hol vannak azok a folyamatosan kisugárzott fotonok? A kérdés nagyon helytálló és jogos is.. Több szempontból is..
Egyrészt nem "látjuk" ezeket a fotonokat, akkor honnan tudhatjuk, hogy vannak?
Másrészt ha folyamatosan kisugározza minden spinnel rendelkező részecske, akkor folyamatosan kellene energiát veszíteniük, aminek az lehetne a következménye, hogy előbb vagy utóbb elfogy az energia készletük.
Nos, igen. Ahhoz valóban nagyon kicsiny lehet az energiája a spin centripetális gyorsulásának hatására kisugárzott fotonoknak, hogy "látható" - érzékelhető hatást váltsanak ki. Ezért megkülönböztetésül ezeket a fotonokat nevezzük Mikro Energiájú Fotonnak, azaz röviden MEF-nek. Ha viszont a forrást azaz a MEF sugárzó részecskét gyorsulásnak tesszük ki, akkor a folyamatos MEf áram térben és időben a rel.Dopplernek megfelelően
"sűrűsödik" azaz térben is időben jól behatárolható csomagokká formálódik. Ezeket a MEF csomagokat már érzékeljük. Ezeket a MEF csomagokat nevezzük fotonoknak.
A logika szerint ha a gyorsulással egyenesen arányos a sűrűsödés mértéke, akkor a fotonok, azaz a MEF sűrítmények energia tartalmának is egyenesen arányosnak kell lennie a gyorsulással. És lőn csoda.. Ha fogunk egy vezetőt (nevezzük antennának), és különféle gyorsulással változó elektromos áramot vezetünk át rajta, akkor a képződött fotonok energiája ténylegesen egyenesen arányosan változik az elektronáramra ható gyorsulással.
Azaz a mérési tapasztalat szerint a Planck által levezetett összefüggés: E=h*f érvényes a MEF sűrűsödésekre.
Már csak az a kérdés maradt nyitva, hogy honnan van mind erre energiája a spinnel rendelkező részecskéknek?
Ez is egyszerű.. Ha egyik spinnel rendelkező részecske sugárzó, akkor az általa kisugárzott MEF előbb vagy utóbb elér egy másik részecskét. Így a részecskék mindegyike egyben MEF kisugárzóként és egyben MEF elnyelőként egyensúlyi állapotban van-lehet.. Amely egyensúly következtében az energia vesztesége egy-egy részecskének nagyon csekély lehet.. Ha pedig a részecskék gyorsulása következtében létrejövő ME fotonok sűrűsödések azaz az általunk fotonnak nevezett energia csomagok találnak el egy-egy részecskét, akkor sok-sok MEF energiáját kapja a részecske egy adagban.. egy nagyon rövid időszakasz alatt.
Azaz az esetleges energia hiányát automatikusan pótolja a foton energiájának "megvámolásával"..
Miután a jelenleg használt mérő módszereink, műszereink érzékenysége nem tudja kimutatni egy-egy fotonnak azt az energia veszteségét amit a spinnel rendelkező részecske a MEF kisugárzása során fellépő energia veszteségének pótlására elvesz, így sajnos jelenleg nem érzékeljük a fotonoknak az energia csökkenését illetve, esetleges energia növekményét sem. Hogy teljesen pontos legyek, tudunk a fluktuációkról, de ezeket statisztikai valószínűségekkel, vagy éppen virtuális fotonok létével magyarázzuk jelenleg. Ha pedig megemlítettem a virtuális fotonok "létét".. akkor illik hozzá tennem, hogy a ME Fotonok alkalmazása esetén a jelenleg "sántikáló" QED modellünk, is végre két stabil lábra állítható a MEF alkalmazásával. Szövegesen kifejtve "röviden" ennyi.
Talán még érdemes azt hozzá tenni, hogy Einstein a ON THE ELECTRODYNAMICS OF MOVING BODIES című művében úgy fogalmazott, hogy azért kell nagyon lassan gyorsítani, azaz nagyon kis gyorsulást alkalmazni, hogy ne legyen energia kisugárzása az elektronnak.
Nos, ezzel érdekes módon azt a látszatot keltette, hogy ha egy töltéshordozóra gyorsulás hat, akkor a gyorsulásnak van egy alsó határa amely alatt nem jön létre a foton kisugárzás. Pedig ilyen határról szó sincs. Ő sem definiált ilyen határértéket, és az utódainak sem sikerült ilyen legkisebb még sugárzásra kényszerítő gyorsulás érték definiálása. Így miután a nulla gyorsulást végtelenül megközelítő gyorsulás értékek esetében is van foton kisugárzás, az így kisugároztatott fotonok energiája szintén végtelenül kicsiny, a mérések nagyságrendje szempontjából elhanyagolhatóan kicsiny, ezért javasolta Einstein a nagyon kis gyorsulással való mozgásállapot változtatást az elméletében kiindulásként. Ez pedig önmagában felveti annak a gondolatnak a lehetőségét is, hogy Einstein is tisztában volt a MEF létének lehetőségével. Nagy kárnak vélem, hogy nem fejtette ki, nem foglalkozott az ebben rejlő lehetőségekkel. Így meghagyta számomra ezt a jeles lehetőséget.
Ezúton fejezem ki köszönetemet Albert Einstein, Max Planck és Hendrik Lorentz tudós uraknak!
Az Ő munkásságuk nélkül nem jöhetett volna létre a tömeg tehetetlenségét ennyire egyszerűen megmagyarázó leírásom.
Köszönet Nekik, és hála a fáradozásukért!

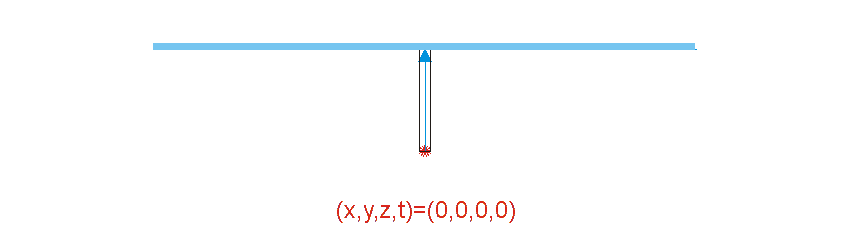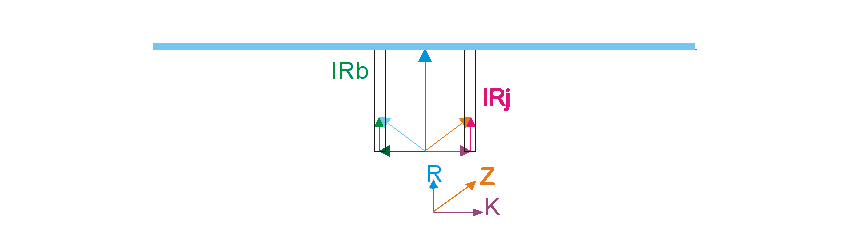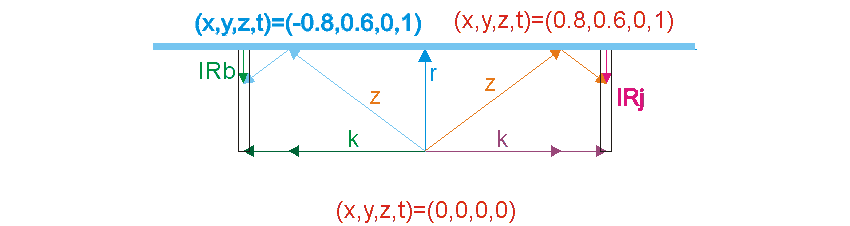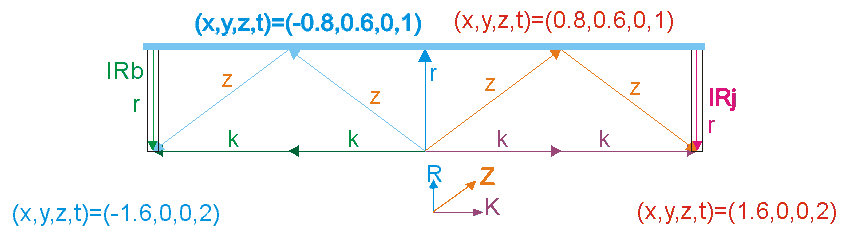


.jpg)




.gif)
.jpg)
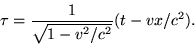


.jpg)
.jpg)
.jpg)

.jpg)